MI Ma’arif Kaliwedi 01

Mungkin banyak orang yang belum kenal tentang MI Ma’arif Kaliwedi 01 yang bertempat di Rt. 02/4 Kaliwedi Kebasen yaitu timur lereng gunung kendeng .Pada tanggal 16 juni 2013 MI Ma’arif Kaliwedi 01 yang bertempat di grumbul ngasinan mengadakan wisuda anak kelas 6 tersebut dengan acara bazar , lomba balita ,jalan sehat dan di iringi oleh marching band . Balai desa kaliwedi sebagai start awal dan peserta langsung kearah utara menuju ngasinan dan melalui kaliwedi lor . Masyarakat kaliwedi lor antusias sekali menyambut acara wisuda so banyak anak kaliwedi lor dan sekitarnya yang sekolah di MI ngasinan tersebut . Jalan menuju MI 1 Kaliwedi yang dari arah barat yaitu lereng gunung kendeng sekarang lagi di perlebar , mungkin dengan pelebaran jalan masyarakat kaliwedi lor semakin banyak yang mengarahkan anaknya untuk sekolah di MI di samping itu terdapat materi agama sebagai bekal anak .

sinau aljabar abstrak

belajar aljabar abstrak grup , mungkin orang terlalu apatis dengan ini . menganggap sesuatu itu sulit padahal hal mudahpun akan terasa sulit jika yang pertama dipikirkan adalah kata sulit , yakinlah bahwa kita mempunyai kemampuan .

Pengertian Grup
Struktur aljabar adalah suatu himpunan tidak kosong S yang dilengkapi dengan satu
atau lebih operasi biner. Jika himpunan S dilengkapi dengan satu operasi biner * maka
struktur aljabar tersebut dinyatakan dengan (S,*) dan jika S dilengkapi dengan dua operasi
biner * dan ° maka struktur aljabar tersebut dinyatakan (S,*, °) atau (S, °,*).

Definisi 1.:
1. Operasi biner * pada S adalah jika “a, b Î S berlaku a*b Î S, atau sering dikatakan
Operasi * pada S bersifat tertutup
2. Jika Operasi * pada S tertutup maka (S,*) disebut Grupoid yaitu struktur aljabar
dengan satu operasi yang tertutup (biner).
3. Operasi biner * pada S dikatakan assosiatif jika “a, b, c Î S, (a*b)*c = a*(b*c)
4. Grupoid (S,*) disebut semigrup jika Operasi biner * pada S assosiatif
5. Himpunan S terhadap operasi * dikatakan mempunyai elemen identitas e jika $e Î S,
“a Î S, a*e = e*a = a
6. Semigrup (S,*) disebut monoid jika S terhadap * mempunyai elemen identitas e.
7. Himpunan S terhadap operasi * dikatakan komutatif jika “a, b Î S, a*b = b*a

Definisi 2. :
Misalkan G adalah himpunan tidak kosong dilengkapi dengan operasi . maka struktur
aljabar (G,.) disebut Grup jika dipenuhi aksioma-aksioma berikiut :
a. Tertutup, artinya “a, b Î G berlaku a.b Î G
b. Asosiatif, artinya “a, b, c Î G berlaku (a.b).c = a.(b.c)
c. Mempunyai elemen identitas ditulis e, artinya (“a Î G) a.e = e.a =a
d. Setiap elemen mempunyai invers dinotasikan a-1 adalah invers dari a, artinya (“a Î G)
($a-1 Î G) sehingga a-1.a = a.a-1 = e

Definisi 3.:
G dikatakan grup komutatif atau abelian jika dan hanya jika G Grup dan bersifat
komutatif (“x,y Î G, x.y = y.x )
Contoh :
1. (Z,+) dengan Z = Himpunan bilangan bulat adalah merupakan grup komutatif
2. (Q,+) dengan Q = himpunan bilangan rasional adalah merupakan grup komutatif
3. (R,+) dengan R = himpunan semua bilangan real adalah merupakan grup komutatif
4. (Z,x) bukan merupakan grup sebab aksioma d. tidak terpenuhi, yaitu $2 Î Z, “a Î Z,
2xa ¹ 1 dengan 1 elemen identitas terhadap x
5. (Q,x) bukan merupakan grup sebab aksioma d. tidak terpenuhi, yaitu $0 Î Q, “a Î Q,
0xa ¹ 1 dengan 1 elemen identitas terhadap x
6. (Q-{ 0 }, x) merupakan grup komutatif

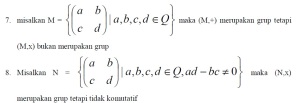
9. (Z,-) bukan grup sebab tidak berlaku sifat asosiatif
10. misalkan G = {0, 1, 2} adalah himpunan bilangan bulat modulo 3 terhadap operasi
penjumlahan modulo 3 disajikan dengan tabel Cayley berikut:

Soal :
1. dari contoh no. 7 di atas, berikan alasan mengapa (M,x) bukan merupakan grup
2. dari contoh 8. di atas, berikan alasan mengapa (N,x) merupakan grup tetapi tidak abelian
3. Himpunan semua himpunan bagian dari S ditulis P(S) = { A | A Ì S} adalah merupakan
power set dari S. Jika S = { p, r, s }dan didefinisikan operasi penjumlahan pada P(S) :
A + B = (AÈB) – (AÇB), “A, B Î P(S) maka :
a. Tunjukkan bahwa P(S) adalah grup, dengan membuat tabel cayley P(S) terhadap
operasi penjumlahan tersebut, selanjutnya, tentukan elemen netral P(S), serta invers
semua elemennya
b. Jika S sembarang himpunan, tunjukkanlah dengan aljabar himpunan bahwa P(S)
adalah grup dan tentukan invers dari sebarang A Î P(S)
c. tunjukkan P(S) merupakan grup komutatif
4. Jika K = { a + bÖ5 | a atau b bilangan rasional tak nol}, dengan operasi perkalian biasa,
maka selidiki apakah K merupakan grup komutatif?
Tugas kelompok : membuat contoh grup dan contoh bukan grup (tidak hanya dalam Z)
yang ditulis dalam plastic transparan atau file.